
***FREE*** Advanced Certified Scrum Master Training Course ***FREE***
We find various applications of “fluid mechanics” in our everyday surroundings. Fluids are mainly classified as either liquid or gas. Everything from a small water flow to car fuel, aerospace industry, air conditioning, and refrigeration requires fluid mechanics. Thus, our lives are obviously connected to fluid flow. Proper understanding of the concept behind fluid mechanics enables us to make the most out of it such as innovative applications. Then why not learn fluid mechanics from basics?
As you go through this article you can gain insight on fluid flow systems, characteristics of fluid flows, fundamental principle, and governing equations, as well as applications of fluid mechanics.
Before getting into deep, let’s distinguish the two words mechanics and dynamics related to fluid systems. “Fluid mechanics” is a study of the behavior of fluids that emphasizes moving fluids and fluids at rest. On the other hand “fluid dynamics” is a subfield of fluid mechanics and it explains the motion of fluid considering the forces that cause the motion. The gist of the article is about moving fluids or fluid flow systems.
Let’s start the journey from fundamentals.
What is fluid flow?
Fluid flow is non-other than the movement of liquids and gases. Learning about fluid flow is interesting, but at the same time, it is complex too. The flow pattern of a fluid depends upon various factors such as characteristics of fluid and speed of the flow. There are mainly two types of flow patterns which are called laminar and turbulent.
Figure 1 – Types of flows
The laminar flow has a smooth, steady fluid motion while turbulent flows are more chaotic. The “laminar” flows in parallel layer and the “turbulent flow” is identified by its irregular movements.
There are three characteristics of fluids namely compressibility, viscosity and density. Since we are going to use these words throughout the article, let’s discuss them one by one.
Compressibility – Ability to compress a fluid into a smaller volume. Liquids are called incompressible fluids since a liquid is hard to compress. However, gas is easy to compress. So gasses are compressible fluids.
Viscosity – Viscosity of a fluid is known as resistance to flow. The best example for this characteristic is water and honey. Honey has more viscosity than water as it doesn’t flow easily.
Density – As we all know, the density is defined as mass per unit volume. The gasses have much lesser density compared to liquids.
A fluid without either compressibility or viscosity is called as an ideal fluid.
Our Favourite Agile Books
We found these books great for finding out more information on Agile Scrum:
Conservation Laws
There are a lot of mathematical models and equations that explain the movement of fluid flow. In order to understand them correctly, you must know the fundamental theories shown below.
Conservation of Mass
“The conservation of mass states that mass cannot be created or destroyed”. And the mass of any system must remain constant over time.
Conservation of Energy
“The conservation of energy states that the total energy of an isolated system remains constant”.
While keeping these theories in mind, let’s move into a set of equations that you really should be aware of when dealing with fluid mechanics.
Continuity Equation
The continuity equation is an application of the principle of conservation of mass. In order to derive the continuity equations, let’s apply the principle of conservation of mass to the following system.
Figure 2 – Continuity for Fluids
The above image shows a cross-section of a pipe that has a single inlet and a single outlet. According to the principle of conservation of mass, the mass inflow rate must be equal to the mass outflow rate. Assume that the fluid is steady, incompressible and non-viscous.
If we do the math for a particular time interval delta t(),
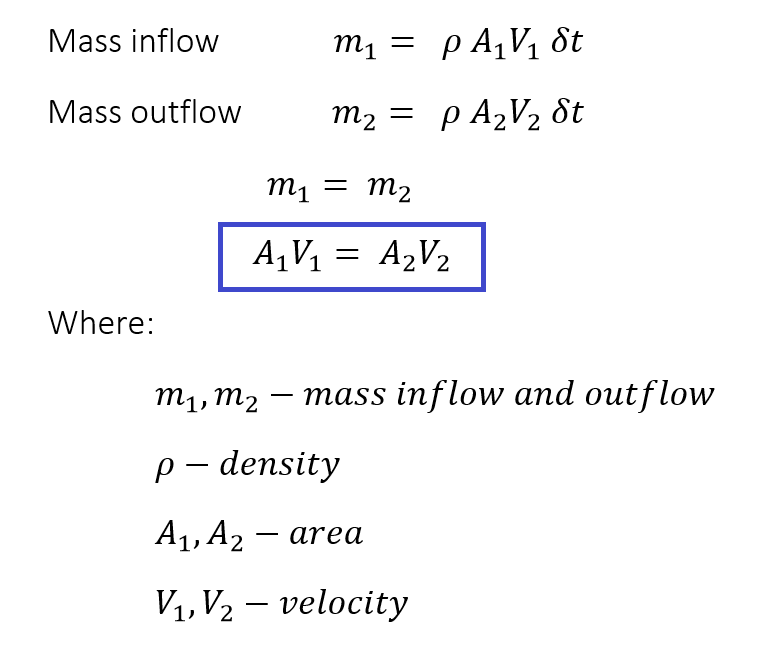
Equation1 – Continuity Equation
The inlet of the pipe has a larger cross-sectional area compared to the outlet. When the cross-section of the pipe gets smaller, the velocity of the fluid increases. You have probably experienced it when watering the plant using a garden hose. Using the thumb, we can block a part of the nozzle. When the nozzle gets narrower, the speed of the water increases.

Euler’s Equation of motion
Euler’s equation of motion gives us the relationship between the velocity, pressure, and density of a moving fluid. The following image shows a steady flow of an ideal fluid element along a streamline. There is no energy or forces (except pressure and gravity) are involved in the flow.
Figure 3 – Euler’s equation diagram
Here is the Euler’s equation of motion in the form of a differential equation. It is derived based on Newton’s second law of motion assuming fluid is non-viscous, incompressible, steady and continue along a streamline.

Equation 2 – Euler’s equation of motion
We can simply derive the Bernoulli’s equation by integrating the Euler’s equation of motion.
Bernoulli’s Equation
This is the most famous equation in fluid mechanics. Bernoulli’s equation nicely represents the concept of conservation of energy. Have a look at an example given. The below diagram shows an incompressible fluid moving inside a pipe. The cross-sectional area and the height of the openings are different.
Figure 4 – Bernoulli’s equation diagram
According to the principle of conservation of energy, the total energy of the fluid must be equal at any two points. Then we can equate the energy of the two different points as shown below. Since the energy is not created nor destroyed, the total energy of the moving fluid is a constant value along the streamline.

Equation 3 – Bernoulli’s Equation
Assume that, you have a horizontal pipe. So there is no gravitational potential energy involves in the equation. If we increase the pressure of the fluid, to maintain a constant value, the velocity will be decreased. Decreasing the pressure will make the velocity increase.
Do you want to know the secret behind an airplane? Even though there are a lot of applications and real-life examples of Bernoulli’s Principle out there, let’s find how it allows planes to fly high.
Figure 5 – Wing of an airplane
It happens with the architecture of the wing of the plane. As you can see above, the bottom face of the wing is flat and the top of the wing has a little curve. That design makes air to flow slower at the bottom while creating more pressure compared to the top face. It will lift the plane up and makes the plane fly.
Generally, Bernoulli’s equation used for steady and laminar flow and fluid must be ideal and incompressible. To avoid those limitations the energy equation, which takes care of viscosity, density, pressure and velocity variant of a fluid, is introduced.
Energy Equation
Since the Bernoulli’s equation doesn’t take any other form of energy into accounts, such as pump work and turbine work, the energy equation comes into the action. To apply the energy equations, the fluid flow doesn’t have to be incompressible or non-viscous.

Equation 4 –Energy Equation
The energy equation is useful when determining hydraulics and energy grade lines of a fluid system. In the next section, let’s talk about the energy grade line and hydraulic grade line.
Hydraulic and Energy Grade Lines
Hydraulics and Energy Grade Lines are imaginary lines that help engineers to graphically visualize and find trouble spots in complex pipe systems.
Figure 6 – Grade lines in a straight pipe
The energy grade line indicates the total energy of the fluid system, and the hydraulic grade line indicates the pressure along the pipe.

Equation 5 – Hydraulic and Energy Grade Lines
Hope this helped you well to acquire fundamental principles of “fluid flow systems”. Now it’s time to discover some interesting applications and benefits of learning fluid mechanics. Here they are,
- Useful when designing canal and dam systems.
- Hydraulic machinery.
- Pipe networks
- Automotive Industry: starting from car fuel to functionality in engines
- Biomedical Applications
- Aerospace and aerodynamics
- Renewable energy systems: wind turbines
